Les vecteurs

Utiliser la notation $\lambda{u}$
Etablir la colinéarité de deux vecteurs.
Caractériser l'alignement par la colinéarité de deux vecteurs
Caractériser le parallélisme par la colinéarité de deux vecteurs

IProduit par un nombre réel

1Interprétation géométrique

Multiplier un vecteur par un nombre réel revient simplement à alonger sa norme (utiliser le curseur ci-dessous pour faire varier $k$) :

Soit $k$ un nombre réel et $\vec{u}$ un vecteur quelconque. Le vecteur $k \times \vec{u}$ a :

Même direction que $\vec{u}$
Même sens que $\vec{u}$ si $k \gt 0$ ou sens opposé si $k \lt 0$
sa norme égale au produit de celle de $\vec{u}$ par $k$

Multiplier un vecteur $\vec{u}$ par $-1$ donne le vecteur opposé $-\vec{u}$

2Calcul sur les coordonnées

De même que pour la somme de deux vecteurs, ici les coordonnées des vecteurs nous permettent également de traiter la multiplication par le calcul.

Soient $\vec{u} = \left ( \begin{array}{c} x \\ y \end{array} \right ) $ un vecteur et $k$ un nombre réel. Les coordonnées du vecteur $k \vec{u}$ se calculent simplement de la manière suivante : $$ k \times \vec{u} = \left ( \begin{array}{c} k \times x \\ k \times y\end{array} \right ) $$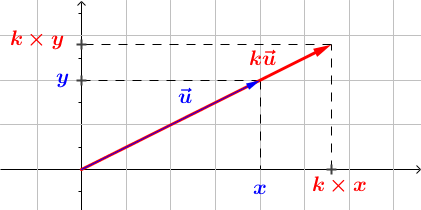

On considère le vecteur $\vec{u} = \left ( \begin{array}{c} 2 \\ 1 \end{array} \right )$, représenté ci-dessou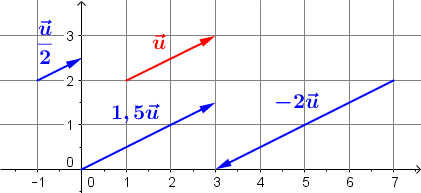s :

On, calcule les vecteurs suivants :

$1,5\vec{u} = \left ( \begin{array}{c} 3 \\ 1,5 \end{array} \right )$

$-2\vec{u} = \left ( \begin{array}{c} -4 \\ -2 \end{array} \right )$

$\frac{1}{2}\vec{u} = \left ( \begin{array}{c} 1 \\ 0,5 \end{array} \right )$

IIColinéarité, parallélisme, alignement